淺談取樣定理
Table of Contents
1 來個取樣的思想實驗
想像你的房子剛好有個窗子,能看到窗外有個摩天輪,這個摩天輪有 360 個座位,以逆時針方向依序編號,但不巧,你的視角只能看到一台車。如果你固定兩個小時的整點觀察一次該摩天輪,發現每次都是編號第 180 的車,請問該摩天輪的轉速是多少?還是該摩天輪根本就沒轉呢?
那麼如果你增加觀察的頻率,固定每個小時的整點都觀察一次該摩天輪,發現這次不一樣了,每個小時觀察到的車輛編號是 0, 180, 0, 180 交替出現,那這代表什麼呢?恭喜你,至少確定排除摩天輪不轉的可能性。那麼該摩天輪的轉速到底是多少呢?每兩個小時觀察到他會轉一整圈,那麼是每小時半圈嗎?答案是:不一定。
這次我們換個角度來想,已知摩天輪每兩個小時轉一整圈,那麼你最少要用多快的觀察頻率,才能知道摩天輪的正確轉速?
如果你用跟摩天輪轉速相同的頻率,也就是每兩個小時觀察一次,那你會跟第一段的觀察結果一樣,看到每次都一樣的車輛編號,導致你根本就不知道他到底是有轉還是沒轉。那如果你用每個小時觀察一次,也就是兩倍於摩天輪轉速的頻率來觀察,那你會看到跟第二段一樣的結果,也就是每個小時剛好是相反的位置被觀察到,換算成轉速是每小時 0.5 圈,那如果變成四倍,也就是每 30 分鐘就觀察一次呢?摩天輪每兩個小時轉一整圈,那每 30 分鐘就是轉 1/4 圈了,那你會看到 0, 90, 180, 270, 0, 90, 180, 270,換算也是每小時 0.5 圈,看來你已經可以正確觀察到摩天輪轉速了,更高的觀察頻率應該也可以觀察到正確的轉速,你心裡想。可是最少要多少頻率才能觀察到正確轉速呢?
這次我們每一個半小時觀察一次,上一段我們知道每 30 分鐘,摩天輪會轉 1/4 圈,所以每 90 分鐘觀察,摩天輪會轉 3/4 圈的角度,也就是 360 * 3/4 = 270 個車輛,從 0 開始的話,會依序觀察到 0, 270, 180, 90, 0, 270, 180, 90, 0, …….,如果這次是你第一次觀察到的結果,你可能會很興奮的下結論說這個摩天輪每 4*90=360 分鐘轉一圈,而且方向是與編號方向相反方向的。可是我們已經知道摩天輪每兩個小時轉一圈啊,這個結果跟已知不合啊。所以低於轉速兩倍的觀察頻率看來也是不行,有興趣的讀者可以嘗試其他低於兩倍的觀察頻率,看看結果是如何?
那現在同樣的摩天輪,但你搬家了,變成只能看到摩天輪的地面,剛好在編號 0 的車輛上,有一個雷射光束,永遠指著地面,而你能夠觀察到地面的雷射光束位置。
高中數學告訴我們,雷射光束的位置與編號 0 的車子被轉的角度有一個關係,那個關係叫做 \(cos \theta\), 這裡假設摩天輪的半徑是 1,那在地面雷射光束的位置就是 \(cos \theta\) 了,所以地面位置用 +1 到 -1 來表示。
回到摩天輪觀察頻率,如果我們用每兩個小時觀察一次的頻率,我們會看到雷射光束一直都指在同一個地方,為了方便描述,我們就說他一直都是在 +1.0 的位置上。畫成圖就會像圖 1 所示。
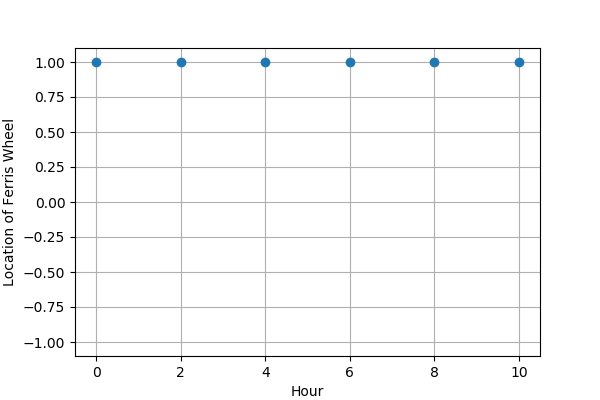
Figure 1: 取樣頻率等於訊號頻率
那如果我們每個小時觀察一次,雷射光束指的位置又會有什麼變化呢?如果我們在相同位置觀察到 0, 180, 0, 180, ……, 那麼第 0 輛車的位置就會在 +1.0, -1.0, +1.0, -1.0, …… 變化了,畫成圖的話就變成:
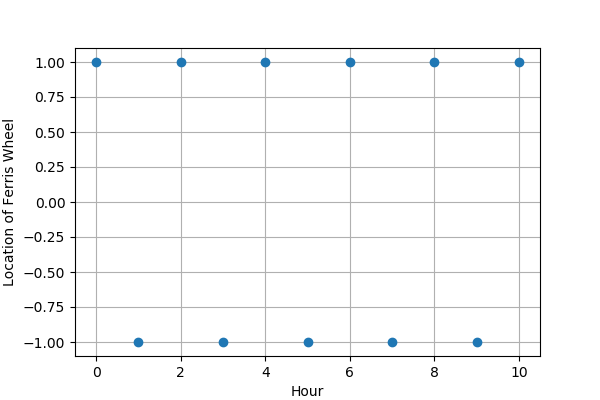
Figure 2: 取樣頻率兩倍於訊號頻率
在訊號處理的領域上,我們習慣將取樣到的點與 X 軸連接起來,來表示它是取樣資料,就像下圖這樣:
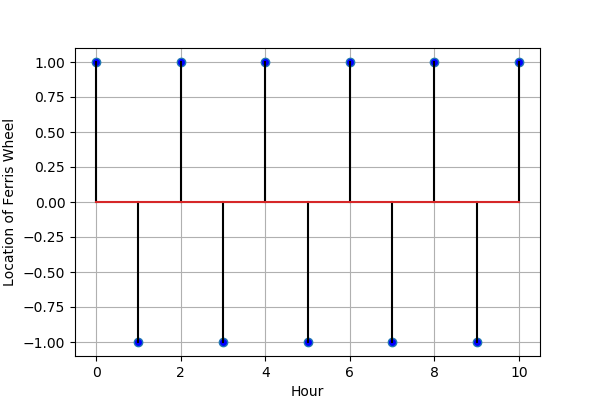
Figure 3: 週期為 2 hr,頻率 \(F = \frac{1}{2}\) cycles per hour 的正弦波,以 \(F_s = 1\) cycles per hour 來取樣(\(F_s = 2*F\))
在圖 3 我們引入了週期以及頻率的觀念,這裡我們用的頻率單位是 cycles per hour,也就是每小時的轉速,轉換成每秒的轉速就變成 \(\frac{1}{3600}\) cycles per second,也就是 \(\frac{1}{3600}\) Hz(Hz 這個單位一直到 1960 年代為了紀念赫茲(Heinrich Hertz) 以後才被廣泛使用,在此之前都是以更直接的 cycles per second 這種一目了然的單位來表示),正弦波的一個週期,就是上述的摩天輪轉一圈回到原點,所以會用 cycles 喔!
那麼如果我們回頭看剛剛那個以 1.5 小時取樣率的結果,畫成圖來看呢?注意算一下圖上的訊號週期就是 6 小時(X 軸的單位就是小時),與我們剛剛計算的結果是一樣的,也就是 360 分鐘轉一圈。
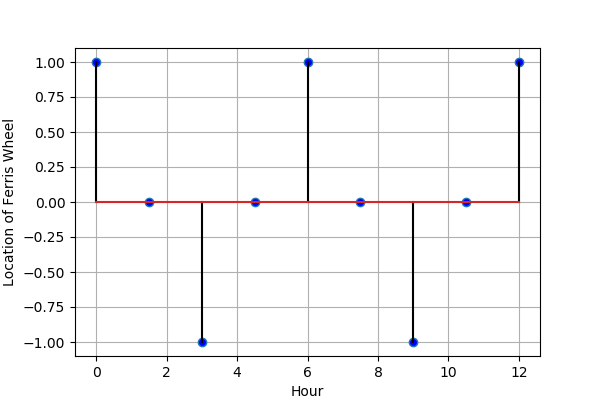
Figure 4: Fs = 1.3333 * F
那我們如果取樣頻率更高一些呢?比方說四倍?我們來看一下結果:
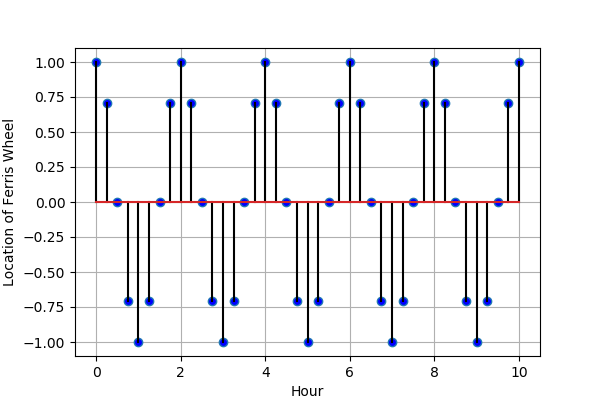
Figure 5: Fs = 4 * F
圖 5 看起來就像是圖 3 的細緻版,只要每四點取一點,就會變成取樣率只有兩倍的那張圖。而這個「每 N 點取一點」也就是訊號處理 decimation 的基本觀念(不過當然不只有這樣,還需要做一些濾波的動作),但這就是基本的取樣率轉換的概念,在這篇文章裡面我們不詳談,有機會筆者再詳細說明。
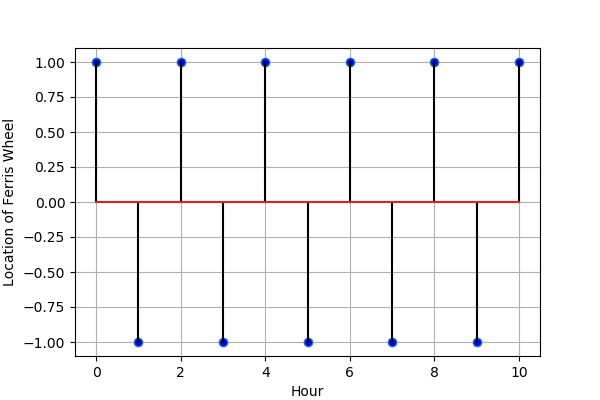
Figure 6: 週期為 \(\frac{2}{3}\) hr 的正弦波,以 \(F_s = 1\) cycles per hr 取樣
回到本文的第二段,為什麼看起來一樣的圖形,不一定代表一樣高的頻率訊號;圖 6 看起來跟圖 3 是完全一樣的圖形,但其實他的原始訊號頻率高三倍,不信我們將取樣率再高一些,變成 3 倍看看,如圖 7 所示。
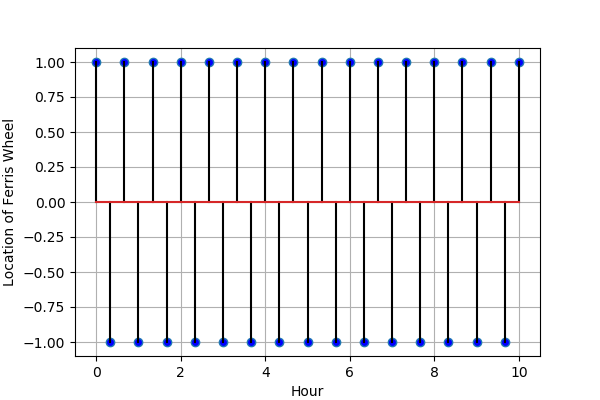
Figure 7: 週期為 \(\frac{2}{3}\) hr 的正弦波,以 \(F_s = 3\) cycles per hr 取樣
這是因為在數位訊號的領域上,不能表示真實的頻率,所有的頻率只剩下 [0, 1] 或是 \([0, 2\pi]\) ,前者稱為 normalized frequency, 單位是 cycles/sample,後者的單位則是 radian/sample,要轉換成真實的頻率,就需要把取樣率考量進來,變成 \([0, \frac{F_s}{2}]\) Hz,所以在數位訊號處理中,取樣率是個非常重要的參數喔!
而圖 6 取樣率是 1 cycles per hour,被取樣的訊號是 1.5 cycles per hour,最後得到的數位訊號是 1 cycles per hour,這個現象稱之為 alias,是我們一般要避免的,但有時候也會刻意採用這種取樣方式,筆者在下一篇文章會講相關的議題。
2 Nyquist Rate
我們常常會聽到某訊號的 Nyquist rate 是多少?其實就是上一段直觀結論的數學版,一個 F 頻率的訊號,要用 \(F_s = 2*F\) 的取樣頻率來取樣,才能夠完整表示這個訊號,這個 \(F_s = 2*F\) 就是 Nyquist rate,有時候這又稱為取樣定理,或是 Shannon Sampling Theorem. 這裡的 Shannon 就是那個 Claude E. Shannon 啦。這起源於 19xx 年代,美國的電話公司開始數位化語音訊號,當時用的是 64kbps PCM(Pulse-Coded Modulation, 是一種用脈衝振幅來代表訊號大小的一個數位傳輸方式),為了節省頻寬,電話公司當然是要研究怎麼樣才能用最少的取樣頻率來傳遞語音訊號,Nyquist 採用的方式比較像是工程師直接量測與觀察得到的結論,而 Claude E. Shannon 則是後期利用取樣與 FFT 的關係,用數學式來描述,所以同樣內涵的取樣定理,有人稱之為 Nyquist Sampling Theorem,也有人稱之為 Shannon Sampling Theorem, 或是 Nyquist-Shannon Sampling Theorem,至於量測得到的結論,與數學式表示誰比較重要,我認為是兩者都重要,因為還沒有什麼理論是不需要實際驗證的,在理論能建構之前,大部分時候,也無法憑空想像出來,因為實驗就是了解上帝所創造的這個世界的方式。歸納永遠比演繹來得早,但歸納與演繹缺一不可;歸納能讓你了解系統現象,演繹則能讓你在腦海中從事思想實驗並大幅推廣。
3 取樣率與取樣頻寬
既然單一頻率的正弦波可以用他的 Nyquist Rate 來正確取樣,那麼所有頻率低於這個頻率的正弦波也可以用同樣的取樣率來取樣,所以我們一般會說 \(F_s \ge 2B\), \(F_s\) 是取樣率, B 是所需的訊號頻寬。
4 那我到底要多少取樣率呢?
是的,了解最低需要兩倍的取樣率之後,在訊號處理領域裡面,永遠都會再繼續問這個問題:到底要多少取樣率才夠呢?取樣率高有什麼好處與壞處?在市面上強調高取樣率的,最常見的就是音效卡,明明已經說了音樂到 20kHz 的頻寬就足夠,而 CD 取樣率也只有到 44.1kHz 而已,但你還是可以看到 96kHz 甚至 192kHz 取樣率的音效卡,那取樣率比 Nyquist rate 高這麼多有什麼用處呢?這有很多實作上的考量,先不談這個,你聽過錄製音樂的 CD 嗎?
5 說個 CD 取樣率 44.1 kHz 的小故事
一般會說人耳能夠聽到的範圍是 20 kHz,各位讀者現在也知道了只要兩倍的取樣率就足夠了,那為什麼 CD 的取樣率是 44.1 kHz 呢?那為什麼 DAT(錄音室比較常見的數位錄音帶)是 48 kHz 呢?根據維基百科,這要講到 1979 年 Sony 出了一台 PCM-1600 的裝置,可以在一般的卡帶上錄數位聲音,上面的取樣率就是 44100 Hz,因此 1980 年制定 CD 的標準的時候,就採用這個取樣率。那麼為什麼是 44100 Hz 而不是 40 kHz 呢?首先,要送進 ADC(Analog-to-Digigal Converter) 之前,要先經過一個低通濾波器,而真實世界的濾波器不會「嘎然而止」,而是會「漸漸停止」,這個「漸漸」就是 transition band,transition band 寬一點,濾波器比較容易設計,所以預留了 2.05kHz 的 transition band,那為什麼不是更多呢?當年電視是 PAL 與 NTSC 的時代,都是類比的,現在也幾乎看不到了,所以以當時的技術來說,44100 Hz 可以同時與 PAL 與 NTSC 相容,因為:
NTSC:
- 245 * 60 * 3 = 44100
- 245 active lines/field * 60 field/second * 3 samples/line = 44100 samples/second
- 每個 field 245 條垂直掃描線(整張畫面的主動掃描線是 490 條,但全部有 525 條,但 NTSC 時代每次只更新半張畫面)
- 每秒 60 field(所以每秒是 30 張)
- 主要使用在北美
- 北美交流電是 110V, 60Hz
PAL:
- 294 * 50 * 3 = 44100
- 294 active lines/field * 50 field/second * 3 samples/line = 44100 samples/second
- 每個 field 294 條垂直掃描線(整張畫面的主動掃描線是 588 條,但全部有 625 條,一樣也是每次只更新半張畫面)
- 每秒 50 fiels(所以每秒是 25 張)
- 主要使用在歐洲
- 歐洲的交流電是 110V, 50Hz
這個其實是相當好的工程範例,說明取捨(trade-off) 的藝術,也因此,當年 Sony 在標準會議上大獲全勝,於是 16 bits 44100 Hz 就 變成了 CD 的標準。1980 年代的日本在電子產業上真是強悍啊。
6 結語
對於數位訊號處理的初學者來說,取樣定理一直都是很難的一個題目,筆者一直都想寫個文章來談談取樣定理,也一直沒有太多心思來思考該如何淺顯的表達。本文的思想實驗是我認為很容易入門的方法,藉由這個思想實驗,讀者可以詳細了解取樣的動作,以及取樣會發生的效果,進而了解取樣定理所要描述的內容。取樣其實還有很多其他的題目可以探討,筆者希望這是一篇能夠讓讀者不至於懼怕取樣定理的一篇文章。